What is PSI?
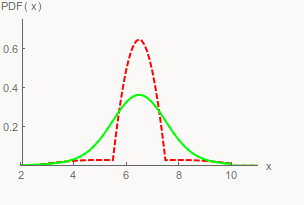PSI is a solver which takes as input a probabilistic program and automatically computes the exact probability density function (PDF) represented by that program. To compute the PDF, PSI uses symbolic inference techniques. It handles probabilistic programs with both discrete and continuous distributions. PSI assumes that loops in the probabilistic program are of finite length.
PSI's ability to compute exact PDFs is in contrast to almost all existing techniques which are approximate in nature (these use sampling or variational methods).
The PDF computed by PSI can be used for a variety of queries, including computing the probability of assertions, expectations, performing inference, computing differences, quantifying the loss of precision, and others. Because of this, PSI is a useful platform for encoding applications from various domains that require probabilistic reasoning.
Download
PSI is available on GitHub. To build and run it, follow the instructions in the README included in the repository.
Publications
The following paper describes the method behind the PSI solver:
- PSI: Exact Symbolic Inference for Probabilistic Programs
[PDF]
CAV'2016 (includes Appendices)
Timon Gehr, Sasa Misailovic, Martin Vechev - Original CAV artifact
For reference, here is the artifact submitted to CAV (which was approved): Artifact with Source Code, Benchmarks and Documentation. (Note: The included version of PSI is out-of-date and performs significantly worse.)
